منذ فجر الحضارة، سعى الإنسان لفهم العالم من حوله، مستخدماً الرياضيات لقياس وتنظيم محيطه. أحد أهم المفاهيم الأساسية في الهندسة هو “محيط مستطيل الرياضيات”، ذلك الشكل البسيط الذي يزخر بتطبيقات عملية واسعة النطاق وهو ما نوضح فيما يلي من خلال منصة جامعة المنح للتعليم الإلكتروني.
Contents
ما هو محيط المستطيل؟
ببساطة، يُعرّف محيط المستطيل على أنه مجموع أطوال أضلاعه الأربعة. فلو كان لدينا مستطيل بطول 5 سم وعرض 3 سم، فإن محيطه سيكون:
محيط المستطيل = 5 سم + 3 سم + 5 سم + 3 سم = 16 سم

الصيغة الرياضية لمحيط المستطيل:
يمكن التعبير عن محيط المستطيل رياضياً باستخدام الصيغة التالية:
محيط المستطيل = 2 × (الطول + العرض)
حيث:
محيط المستطيل: هو المسافة التي تحيط بالشكل.
الطول: هو أطول ضلع في المستطيل.
العرض: هو أقصر ضلع في المستطيل.
خصائص محيط المستطيل:
يُقاس محيط المستطيل بوحدة الطول، مثل السنتيمتر أو المتر.
لا يعتمد محيط المستطيل على زواياه، حيث أن جميع زواياه قائمة (90 درجة).
يكون محيط المستطيل أكبر من ضعف عرضه، وأصغر من ضعف طوله.
إذا كان طول المستطيل يساوي عرضه، فإن الشكل يصبح مربعاً، ويكون محيطه 4 × طول الضلع.
تطبيقات محيط المستطيل:
يُستخدم محيط المستطيل في العديد من التطبيقات العملية، نذكر منها:
حساب كمية السياج اللازمة لتسييج حديقة مستطيلة الشكل.
حساب كمية الخيوط اللازمة لخياطة حواف غطاء مستطيل.
حساب المسافة التي يقطعها شخص عند المشي حول ملعب مستطيل الشكل.
حساب كمية الطلاء اللازمة لتغطية سطح مستطيل.
حساب حجم الصندوق المستطيل.
أمثلة على استخدام محيط المستطيل في الحياة اليومية:
حساب محيط نافذة مستطيلة الشكل.
حساب محيط باب مستطيل الشكل.
حساب محيط لوحة فنية مستطيلة الشكل.
حساب محيط طاولة مستطيلة الشكل.
حساب محيط ملعب كرة قدم مستطيل الشكل.
محيط المستطيل وعلاقته بالمساحة:
تُعرّف مساحة المستطيل على أنها حاصل ضرب طوله في عرضه. وترتبط المساحة بمحيط المستطيل من خلال العلاقة التالية:
مساحة المستطيل = (محيط المستطيل / 4) – (الطول × العرض)
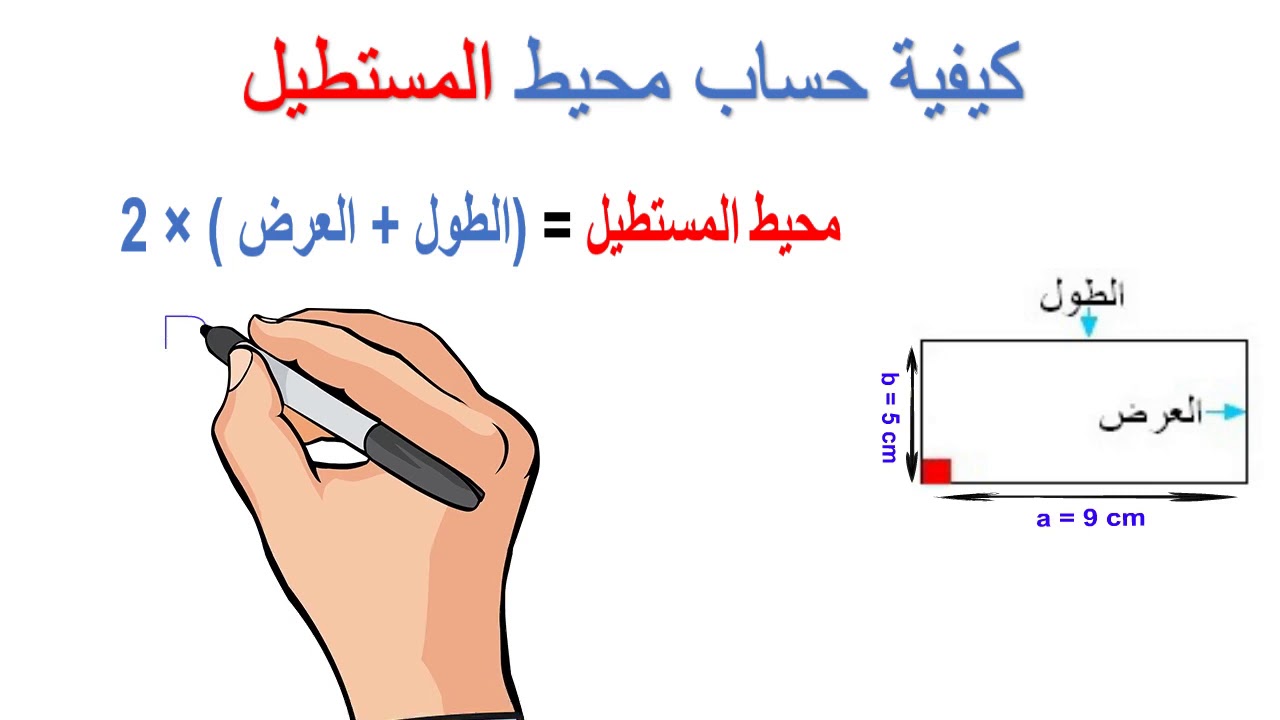
أمثلة على حساب محيط المستطيل:
- إذا كان طول المستطيل 10 سم وعرضه 5 سم، فما هو محيطه؟
الحل:
محيط المستطيل = 2 × (10 سم + 5 سم) = 30 سم
- إذا كان محيط المستطيل 40 سم وعرضه 8 سم، فما هو طوله؟
الحل:
الطول = (محيط المستطيل / 2) – العرض = (40 سم / 2) – 8 سم = 12 سم
أمثلة إضافية على استخدام محيط المستطيل في الحياة اليومية:
حساب محيط شاشة الهاتف المحمول.
حساب محيط بطاقة الائتمان.
حساب محيط ورقة A4.
حساب محيط ملعب تنس مستطيل الشكل.
حساب محيط حمام سباحة مستطيل الشكل.
حساب محيط قطعة أرض مستطيلة الشكل.
حساب محيط حوض سمك مستطيل الشكل.
حساب محيط خزانة ملابس مستطيلة الشكل.
حساب محيط لوحة مفاتيح مستطيلة الشكل.
حساب محيط غطاء كتاب مستطيل الشكل.
تطبيقات إضافية لمحيط المستطيل في مجالات مختلفة:
في مجال الهندسة المعمارية: لحساب محيط المباني والغرف والأبواب والنوافذ.
في مجال الهندسة المدنية: لحساب محيط الطرق والجسور والسدود.
في مجال التصميم: لحساب محيط الملابس والأثاث والأدوات المنزلية.
في مجال الرياضة: لحساب محيط ملاعب كرة القدم والسلة والكرة الطائرة.
في مجال الفيزياء: لحساب محيط الأجسام المستطيلة مثل المكعبات والمناشير.
من خلال هذه الأمثلة، يتضح أن محيط المستطيل مفهوم ذو تطبيقات واسعة النطاق في مختلف مجالات الحياة، مما يجعله أداة أساسية لفهم العالم من حولنا.
برهان الصيغة الرياضية لمحيط المستطيل
يمكن إثبات صحة الصيغة الرياضية لمحيط المستطيل (محيط المستطيل = 2 × (الطول + العرض)) باستخدام طريقة التقسيم:
- نرسم مستطيلاً بطول (أ) وعرض (ب).
- نقسم المستطيل إلى أربعة مستطيلات أصغر، كل منها بطول (أ/2) وعرض (ب).
- نلاحظ أن محيط المستطيل الأصلي يساوي مجموع محيطات المستطيلات الأربعة الأصغر.
- محيط كل مستطيل أصغر هو 2 × ((أ/2) + (ب)) = أ + 2ب.
- مجموع محيطات المستطيلات الأربعة الأصغر هو 4 × (أ + 2ب) = 4أ + 8ب.
- نقسم محيط المستطيل الأصلي على 2، ونحصل على 2 × ((أ/2) + (ب)) = أ + 2ب.
- نلاحظ أن هذه المعادلة مطابقة لمعادلة محيط المستطيل الأصغر.
- من خلال هذه الخطوات، أثبتنا أن محيط المستطيل يساوي 2 × (الطول + العرض).
ملاحظة:
يمكن استخدام طرق أخرى لإثبات صحة هذه الصيغة، مثل طريقة التشابه أو طريقة المساحة.
بالإضافة إلى ذلك، يمكن تعميم هذه الصيغة لحساب محيط أي شكل مضلع منتظم.
خاتمة:
يُعدّ محيط المستطيل مفهومًا هندسيًا أساسيًا ذا تطبيقات واسعة النطاق في مختلف مجالات الحياة. من خلال فهم هذا المفهوم، يمكننا حل العديد من المسائل الحسابية، وتصميم الأشكال الهندسية، وإنجاز العديد من المهام العملية.